# from this
layer = nn.Linear(100, 100)
# to this
layer = torch.nn.utils.spectral_norm(nn.Linear(100, 100))Spectral normalization is one of the many kinds of normalization operations that can be used in a deep learning model. In fact, it can be thought of as both a regularization and normalization technique. If you have ever asked yourself what spectral norm does or when we should use it over, say batch normalization, then read on.
Norms and Normalizations
Before we get into Spectral Normalization let’s define what a norm is. According to the Deep Learning Book, a norm is a function used to measure the “size” of vectors. Mathematically, it is a function that maps from a complex vector space to non-negative real numbers. It is denoted with single bar (\(|.|\)) or double bar (\(\|.\|\)). For a function to qualify as norm it has to have 3 properties:
\(|x| = 0\), iff \(x=0\)
\(|kx| = |k|\cdot|x|, k \in \mathbb{R}\)
\(|x + y| \leq |x| + |y|\)
Note that a matrix norm is not the same thing as a vector norm. I must have dozed off during this part in college, but this difference is important for the notation of spectral norm. Usually, vector norms are denoted with \(|.|\) while matrix norms are denoted with \(\|.\|\). For a function to qualify as a matrix norm it needs to follow an extra property:
- \(\|AB\| \leq \|A\|\cdot\|B\|\)
Now lets’s talk about normalization. In the context of deep learning, normalization usually refers to scaling and shifting of either feature maps or weight matrices. For deep models the goal of normalization is to make training easier through some mechanism like reducing internal covariate shift or reducing vanishing/exploding gradients. In deep learning we often use “norm” and “normalization” interchangeably. Batch norm or Instance norm are not “norms” according to the mathematical definition. They are “normalization” methods. That is, they scale internal feature maps to ensure that they have zero mean and unit variance.
“Spectral norm” on the other hand is an overloaded term that can mean both a mathematical norm or a normalization method, depending on the context. In the mathematical norm sense it refers to the largest singular value of a matrix. In the normalization sense, it refers to dividing a matrix by it’s largest singular value (to get a matrix whose singular values are \(\leq 1\)).
If you thought that’s confusing, let’s talk about the mathematical notation for spectral norm. \(L_p\) norms for vectors are usually denoted as \(|x|_p\). The very commonly used \(L_2\) norm, also known as Euclidean norm, is often denoted as \(\|x\|_2\) or simply \(\|x\|\). But, for matrices, the Euclidean norm, also known as the Frobenius norm, is denoted with \(\|A\|_F\), while \(\|A\|_2\) denotes the spectral norm. Not confusing at all!
But seriously, there is a reason for this notation. \(L_p\) norms for matrices is yet another overloaded term that can mean 3 different things(1, 2 and 3). In deep learning when we calculate \(L_p\) norms of n-dimensional tensors, we implicitly refer to the vector norms calculated after flattening the tensor. Wikipedia refers to this as entry-wise matrix norms and denotes it as \(L_{p,p}\) norm for matrices (maybe \(L_{p,p...\text{n times}}\) for \(n\)-dimensional tensors?). Under this more precise definition Euclidean norm is the \(L_{2,2}\) matrix norm while spectral norm is the \(L_{2}\) matrix norm.
Intuition and math
So what does it mean when someone adds “spectral norm” to their deep learning model? It simply means that the weights of the model will be matrices with unit spectral norm. Note that there is no “spectral norm layer” like batch norm or instance norm. Similar to weight normalization, spectral normalization modifies the weights of a linear or convolution layer, instead of its outputs. But what effect does adding spectral normalization actually have on the model? In this section, I will try to explain the intuition behind spectral normalization. Please note that this is only my understanding and I am happy to be corrected if you see any errors.
Singular Value Decomposition
To understand what spectral normalization is doing to a weight matrix we need to look at the singular value decomposition of the weight matrix. As a quick overview, SVD allows us to decompose any matrix \(M\) into a product of 3 matrices\[ M = U \cdot \Sigma \cdot V^T \]
For a real \(M\), the matrices \(U\) and \(V\) are orthogonal and \(\Sigma\) is a diagonal matrix containing the singular values. The singular values are always \(\geq 0\).
Now, if \(M\) is a weight matrix in a neural network, it can also be thought of as a linear transformation acting on an input feature map. In this case, performing SVD on \(M\) allows us to decompose this linear transformation into 3 parts: a rotation, a coordinate scaling and a second rotation. So what happens if we now add the constraint of spectral normalization on \(M\)? We divide \(M\) by \(max(\Sigma)\) to get a new matrix \(M_{norm}\). The singular values of \(M_{norm}\) are in range \([0,1]\). This means that we have limited the ability of our weight matrix to scale the input feature map, while keeping its ability to rotate it unconstrained.
This keeps gradient explosion in check by ensuring each layer scales input feature maps (and gradients in backward pass) by a limited amount. Mathematically this can be expressed by the inequality:
\[ \|M\cdot x\| \leq \|M\|_2 \cdot \|x\| \]
That is, the norm of a vector \(x\) being acted upon by the matrix \(M\) grows by atmost \(||M||_2\) times. Since we have limited \(||M||_2\) to 1, we have limited the amount by which the norm of \(x\) can grow.
This effect is illustrated in the following figures. Fig-1 (taken from here) illustrates the action of a matrix \(M\) on a unit radius disk.
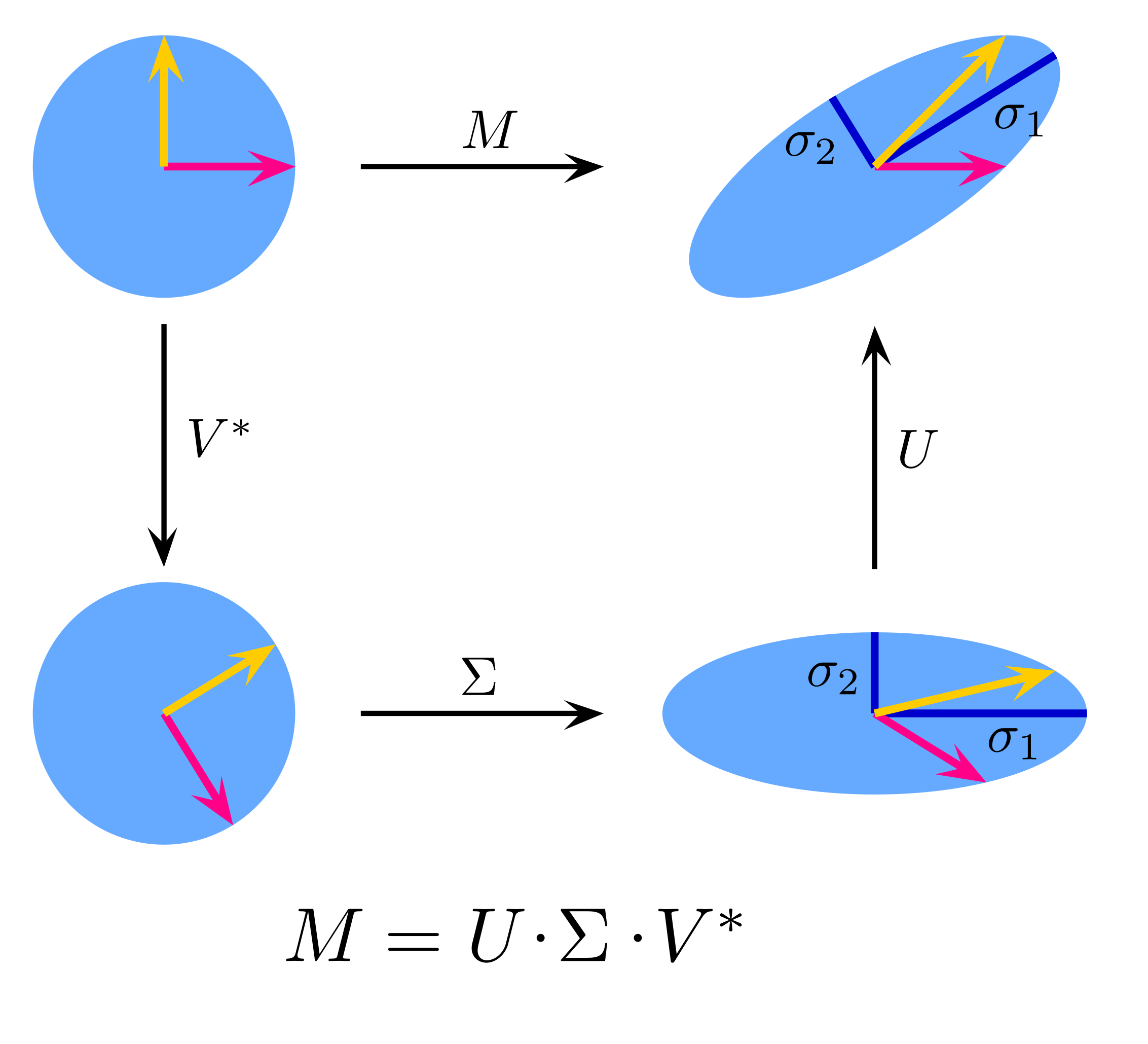
Let us take a vector \(\vec{x_1}\) on this disk. Fig-2 shows how this vector gets transformed by M. After being rotated by \(V^T\), \(\vec{x_1}\) becomes aligned with the x-axis. This means that \(\Sigma\) stretches its entire magnitude by \(\sigma_1\) since the component of \(V^T\vec{x_1}\) along y-axis is \(0\). Since \(U\) is another orthogonal matrix that preserves magnitudes, \(\vec{x_1}\) got the maximum possible magnitude increase after being acted upon by matrix \(M\), and its magnitude is now \(\sigma_1 \cdot |\vec{x_1}|\).
Now let’s prove the inequality mathematically. Let
\[ \vec{x_1} = p\hat{i} + q\hat{j} \]
where \(\hat{i}\) and \(\hat{j}\) are unit vectors along x and y-axes respectively (i.e., they form the orthonormal base for the 2D vector space) and
\[ V^T\vec{x_1} = a\hat{i} + b\hat{j} \]
Since \(V\), and hence \(V^T\), is orthogonal
$$ \[\begin{aligned} |V^T\vec{x_1}| &= |\vec{x_1}|\\ \Rightarrow \; a^2 + b^2 &= p^2 + q^2 = C \end{aligned}\] $$
Now, let \(f = |\Sigma V^T\vec{x_1}| = \sqrt{\sigma_1^2a^2 + \sigma_2^2b^2}\)
We need to maximize \(f\) wrt \(a, b\)
$$ \[\begin{aligned} \underset {a,b}{\operatorname {arg\,max} } \; f^2 &= \sigma_1^2a^2 + \sigma_2^2b^2\\ &= (\sigma_1^2 - \sigma_2^2)a^2 + \sigma_2^2(a^2 + b^2)\\ &= (\sigma_1^2 - \sigma_2^2)a^2 + \sigma_2^2C \end{aligned}\] $$
So, to maximize \(f\) we need to maximize \(a\)
$$ \[\begin{aligned} & \underset {a}{\operatorname {arg\,max} } \; a^2 + b^2 = C\\ \Rightarrow & \; a = \sqrt{C}, b=0 \end{aligned}\] $$
Therefore, the maximum value of \(f = \sigma_1\sqrt{C} = \sigma_1|V^T\vec{x_1}| = \sigma_1|\vec{x_1}|\)
Finally, since \(U\) is also orthogonal,
\[ \max |U\Sigma V^T\vec{x_1}| = \max |\Sigma V^T\vec{x_1}| = \sigma_1|\vec{x_1}| \]
Lipschitz Continuity
While spectral normalization acts as a normalization method by keeping gradient explosion in check, it also acts as a powerful regularization method. This is because several weight matrices \(W\) can map to the same normalized matrix \(W_{norm}\). Thus spectral norm constrains the space of weights.
In fact, spectral normalization constrains neural networks to model only a specific family of functions called Lipschitz continuous functions. A \(K\)-Lipschitz continuous function is a function whose slope between any two points is always \(\leq K\). This \(K\) is called the Lipschitz constant of the function. A neural network with spectral normalization always forms a Lipschitz continuous functions because of the following 3 properties: 1. The Lipschitz constant for linear layers is equal to the spectral norm of their weight matrices. 2. The Lipschitz constant of a composition of functions \(f \circ g \leq\) Lipschitz constant of \(f \times\) Lipschitz constant of \(g\) 3. The Lipschitz constant for activation functions like ReLU and pooling layers is \(1\).
In a neural network with spectral normalization, property 1 ensures that each individual weight layer is \(1\)-Lipschitz while properties 2 and 3 ensure that the entire arbitrary sized model is also Lipschitz continuous. Why is it important to model only Lipschitz continuous functions? The use cases are explained in the next section.
When to use Spectral Normalization?
This is probably the most important part of this post. But unfortunately, like most things in deep learning there is no specific answer to this question. From the intuition above, spectral norm’s purpose can be understood to constrain the weight space of a neural network. It can find a use wherever this property is desired.
Generative models and reinforcement learning
The most common use case for spectral normalization is in GANs. Miyato et al. [1] proved that adding spectral normalization to the layers of a discriminator leads to more stable training of GANs. Here’s how: In GANs, the generator does not directly receve any gradients because we do not have any ground truth for it. The only way it receives gradients is through the discriminator. This is why it is important for the derivative of the discriminator to be bounded, otherwise the generator can become unstable. But the function modelled by a normal neural network doesn’t need to have bounded derivatives.
Enter Lipschitz continuity. As mentioned before, a \(K\)-Lipschitz continuous function is a function whose slope between any 2 points is always \(\leq K\). In other words, these functions have bounded derivatives. Using spectral normalization, we can constrain the discriminator to only model Lipschitz continuous functions.
This concept of Lipschitz continuity doesn’t have to be limited to GANs. If some other application requires this constraint, spectral normalization can help. In fact Lipschitz continuity just refers to “smooth” functions. If a task requires a neural network to model only “smooth” functions, spectral norm is useful.
Zhang et al. [2] went beyond [1] and showed that it is useful to apply spectral normalization to generators as well. While there is no mathematical proof behind why the generator should be regularized, the authors hypothesize that spectral normalization prevents the magnitude of weights from growing too large and prevents unusual gradients.
Gogianu et al. [3] show that applying spectral normalization to a Deep-Q-Network improves performance of reinforcement learning. A Q-Network is a neural network that assigns values to all the actions an agent can take while in its current state. It allows the agent to find an optimal action at every step. Turns out applying spectral norm also helps performance here. The authors also point out that unlike the discriminator of GANs, there is no need for a Q-network to be super smooth. They find it is more beneficial to control the smoothness by applying spectral norm to only a few layers of the network.
Multi-task Learning
In multi-task learning we often have a common body that projects input data to a common latent space, and multiple task-specific heads for task-specific outputs. For these models, it is important for the common latent space to capture information that is useful for all the heads. Otherwise the model won’t do equally well for all the tasks.
A simple way to prevent one task from dominating over others is to apply weights to the losses so that all the losses have gradients that are similar in magnitude. But, tuning loss weights only affects the initial gradients for each task. The final gradients received by the common body is the sum of gradients backpropagated through each task head. If the weights in any one head are such that they scale their gradient to have a disproportionately large magnitude, this task will dominate the final gradients received by the common body. This can make tuning the loss weights non-intuitive. It is possible for spectral normalization to help in this case. Spectral norm when applied to each of the task-specific heads, prevents the weights in each head from scaling the common latent vector too differently (think of each head to be rotating the latent vector without affecting its magnitude too much). This forces the heads to cooperate and prevents any one head from dominating, since if the spectral norm of weights in one head grows disproportionately, the gradients from that head can potentially have a much larger magnitude, causing it to dominate the total gradient.
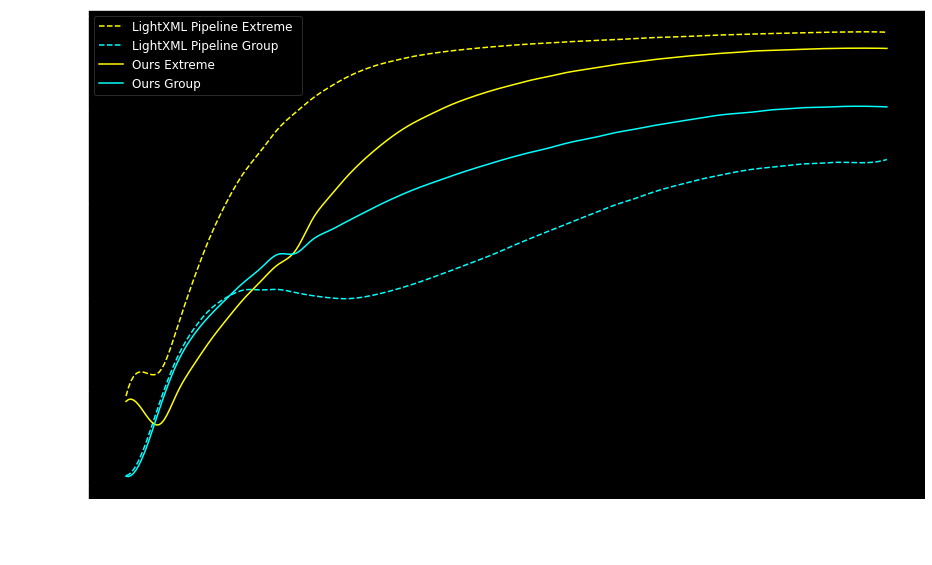
Fig-3 shows a graph from a paper [4] (authored by yours truly) that gives empirical evidence of this phenomenon. Applying spectral norm brings the precision of the 2 different tasks in our model closer together. The dashed lines represent the original pipeline without spectral norm. The solid lines represent our modified training pipeline that uses spectral norm.
Possibly Transfer Learning
The idea of using spectral norm for transfer learning has sort of been proposed by Dahiya et al. in [5]. It is another paper in the same domain as [4]. While our approach was to learn the two tasks in parallel, creating a multi-task problem, [5] learns the tasks sequentially. For this they needed to make sure that when training the model for the second task, it does not lose performance on the first task. To achieve this, they use spectral norm on their weight layers. [5] proves that using spectral norm prevents the initially trained weights from drifting too far away and the model can do well on both tasks.
[5] trains a small model with a single weight layer and applies spectral norm to it. There is a possibility that we can scale up this idea of reducing weight drift to larger models as well. It might be possible to take a CNN pretrained on Imagenet and train it on a new dataset while retaining close to the original performance on imagenet. That is, spectral norm might offer a way to reduce catastrophic forgetting.
To test this I ran some experiments with the MIT Indoor Scene Recognition dataset [6]. This dataset is sufficiently different from Imagenet. Standard pretrained resnet models are not trained with spectral normalization and simply adding spectral normalization to a pretrained model degrades performance. Training on imagenet with spectral normalization is also not a good idea because spectral normalization decreases classification performance over batch norm (because of overly strong regularization). One solution is to take a normal pretrained model and calculate the initial spectral norm of each weight layer as \(\sigma_W\). Now, instead of limiting this spectral norm to be in range \([0,1]\), we can limit it to be in range \([0, \sigma_W]\) ( similar to the approach suggested in [3] and [7] for reducing the strength of regularization of spectral norm). The old batch norm layers can be frozen to act as simple affine layers.
Results were inconclusive with these experiments. Adding this kind of spectral normalization to a classifier causes it to not train at all for the first few epochs and then improve rapidly to match the performance of standard transfer learning, without spectral normalization.
Pytorch implementation
Not much is needed to be said here. “Implementing” spectral norm to a model is as simple as changing one line of code.
A small thing to be noted here is how Pytorch implements spectral norm. First the weight matrix is reshaped to 2D. Then the first vectors of both \(U\) and \(V\) are calculated.
\[ \sigma = u^T \cdot W \cdot v \]
To approximate \(\vec{u}\) and \(\vec{v}\) torch uses the power method. Torch initializes both vectors with random values and performs the following two steps \(n\)-times:
\[ \begin{aligned} \vec{u} &= W \cdot \vec{v} \\ \vec{v} &= W^T \cdot \vec{u} \end{aligned} \]
This calculation happens on every forward pass during train time. During eval, torch uses cached values for \(\vec{u}\) and \(\vec{v}\). Since torch caches the vectors, the state dict of an nn.Module using spectral norm will have two extra keys: ‘weight_u’ and ‘weight_v’. The unnormalized weight is stored with key ‘weight_orig’ instead of ‘weight’ and the normalized weight is calculated on the fly.
Conclusion
To sum up, Spectral Norm is a way to normalize the weights of a deep neural network, instead of its activations. It prevents gradient explosion and, if used on all layers of a network, forces it to model only Lipschitz continuous functions. It can be used for multi-task learning and any other situations where the weights of independent neural networks layers need a “soft tying”.
That said, just like most things in deep learning, your mileage will vary. The regularization produced by spectral norm is quite strong and can hurt performance for “standard” tasks like classification and image segmentation. If your task has no precedent of using spectral norm, use it only if you are feeling adventurous.
References
[1]
T. Miyato, T. Kataoka, M. Koyama, and Y. Yoshida, “Spectral normalization for generative adversarial networks,” ArXiv, vol. abs/1802.05957, 2018.
[2]
H. Zhang, I. J. Goodfellow, D. N. Metaxas, and A. Odena, “Self-attention generative adversarial networks,” in ICML, 2019.
[3]
F. Gogianu, T. Berariu, M. Rosca, C. Clopath, L. Buşoniu, and R. Pascanu, “Spectral normalisation for deep reinforcement learning: An optimisation perspective,” in ICML, 2021.
[4]
S. Kharbanda, A. Banerjee, A. Palrecha, and R. Babbar, “Embedding convolutions for short text extreme classification with millions of labels,” ArXiv, vol. abs/2109.07319, 2021.
[5]
K. Dahiya et al., “DeepXML: A deep extreme multi-label learning framework applied to short text documents,” Proceedings of the 14th ACM International Conference on Web Search and Data Mining, 2021.
[6]
A. Quattoni and A. Torralba, “Recognizing indoor scenes,” in CVPR, 2009.
[7]
H. Gouk, E. Frank, B. Pfahringer, and M. J. Cree, “Regularisation of neural networks by enforcing lipschitz continuity,” Machine Learning, vol. 110, pp. 393–416, 2021.